NA Highlight: Structured iterative methods for waveguide eigenvalue problems
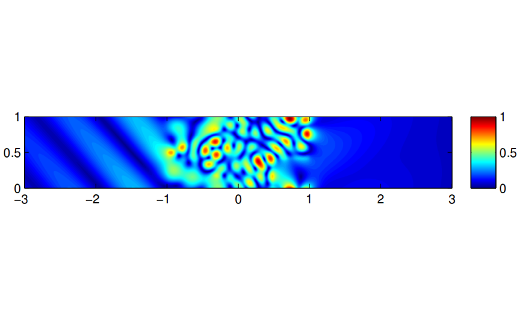
In the field of electromagnetics, certain types of wave propagation can be modeled with waveguides, and can be analyzed by discretizing an associated partial differential equation. The physical domains of the waveguides are typically very large leading to a high computational cost for many direct discretization methods. In this project, we take an approach where the domain is treated as an infinite domain, leading to a nonlinear eigenvalue problems [1]. The nonlinear eigenvalue problem is highly structured and we design iterative methods for this structure. New approaches are developed from a numerical linear algebra perspective, e.g. using Arnoldi’s method and modern iterative methods for linear systems, as well as a perspective of numerical methods for partial differential equations.
References
[1] E. Jarlebring, G. Mele and O. Runborg. The waveguide eigenvalue problem and the tensor infinite Arnoldi method. SIAM J. Sci. Comput., 2017.




