Robust Extraction and Simplification of 2D Tensor Field Topology
Research focus area – Topological methods for dynamical data
Application – Materials for the future
Topological feature analysis is a powerful instrument to understand structural changes in datasets. For tensor fields, e.g. stress fields from material simulations, the topological structure is determined by the distribution isotropic points in the field. One challenge thereby is the high feature density in the data and therefore it is essential to be able to discriminate spurious from important features. In this work, a mathematical foundation for the construction of a feature hierarchy for 2D symmetric tensor field topology has been developed, which is then applied for a controlled simplification of the topological structure. It extends the concept of robustness, quantifying the minimum amount of perturbation to the field that is necessary to remove features, from scalar to tensor fields. An entire pipeline for generating a hierarchical set of degenerate points based on their robustness values has been developed. It includes stable extraction and classification of isotropic points, the computation and assignment of robustness values, and the construction of a simplification hierarchy.
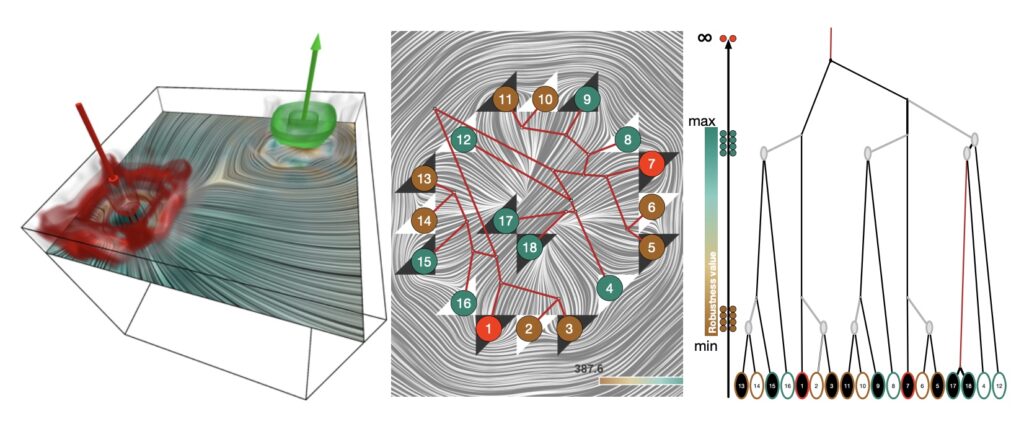
Image: Simulation of a stress field in a solid block with two applied forces. (a) Illustration of the setup with the two forces together with one slice highlighting the direction of the major eigenvector. (b) A textured slice showing degenerate cells that determine the structural information of the eigenvector field. White triangles represent trisectors and black ones represent wedges. The most stable degenerate points are highlighted in red. (c) The tree provides the basis for a hieratical simplification of the field with respect to the stability of degenerated points.
References:
Wang and Hotz. Robustness for 2D Symmetric Tensor Field Topology. In, Modeling Analysis and Visualization of Anisotropy, Springer, 2017.
Jankowai et al. Robust Extraction and Simplification of 2D Tensor Field Topology. In Computer Graphics Forum, 2019.




