Canonical quantum observables for molecular systems approximated by ab initio molecular dynamics

It is known that ab initio molecular dynamics based on the electron ground state eigenvalue can be used to approximate quantum observables in the canonical ensemble when the temperature is low compared to the first electron eigenvalue gap. We have proved in [1] that a certain weighted average of the different ab initio dynamics,  corresponding to each electron eigenvalue, approximates quantum observables for any temperature. The proof uses the semi-classical Weyl law to show that canonical quantum observables of nuclei-electron systems, based on matrix valued Hamiltonian symbols, can be  approximated by ab initio molecular dynamics with the error proportional to the electron-nuclei mass ratio. The result includes observables that depend on correlations in time. A combination of the Hilbert-Schmidt inner product for quantum operators and Weyl’s law shows that the error estimate holds for observables and Hamiltonian symbols  that have three and five bounded derivatives, respectively,  provided the electron eigenvalues are distinct for any nuclei position and the observables are in diagonal form with respect to the electron eigenstates.

[1] Kammonen A., Plecháč P., Sandberg, M. and Szepessy A.,  Canonical quantum observables for molecular systems approximated by ab initio molecular dynamics, Ann. Henri Poincaré (2018) 19,  2727-2781.

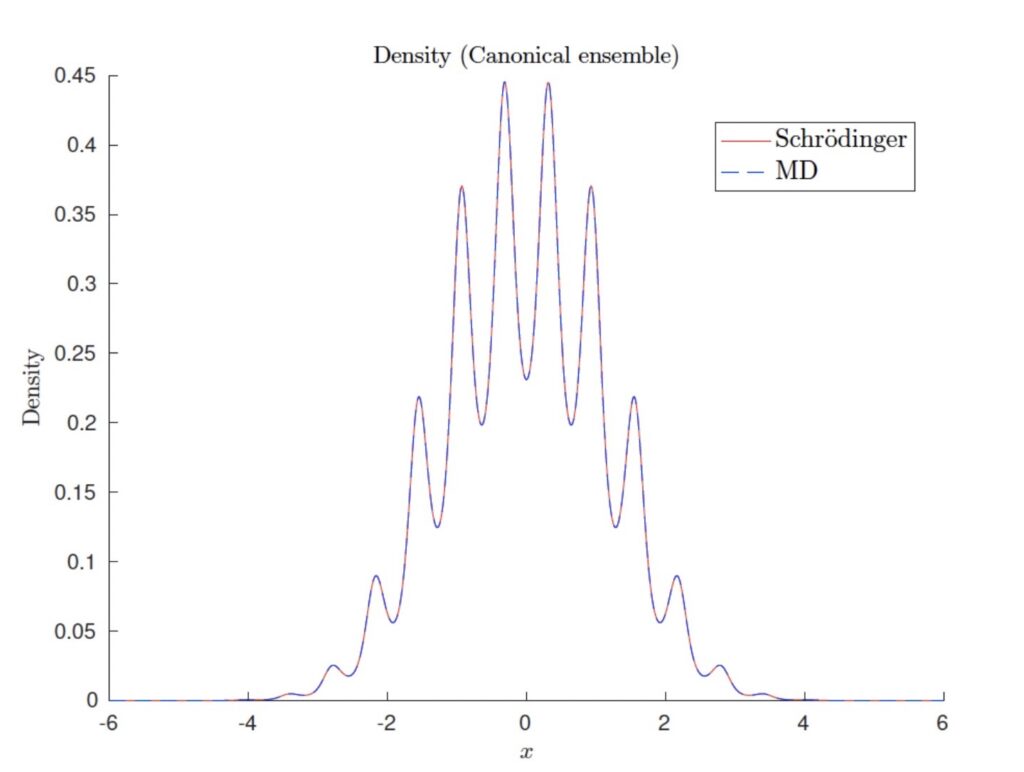
Fig: It is possible to approximate observables in quantum mechanics by molecular dynamics for any temperature. The figure shows that the quantum and  classical  molecular density in the canonical ensemble are almost on top of each other for a model problem.