A Cut Finite Element Method for Incompressible Two-Phase Navier-Stokes Flows
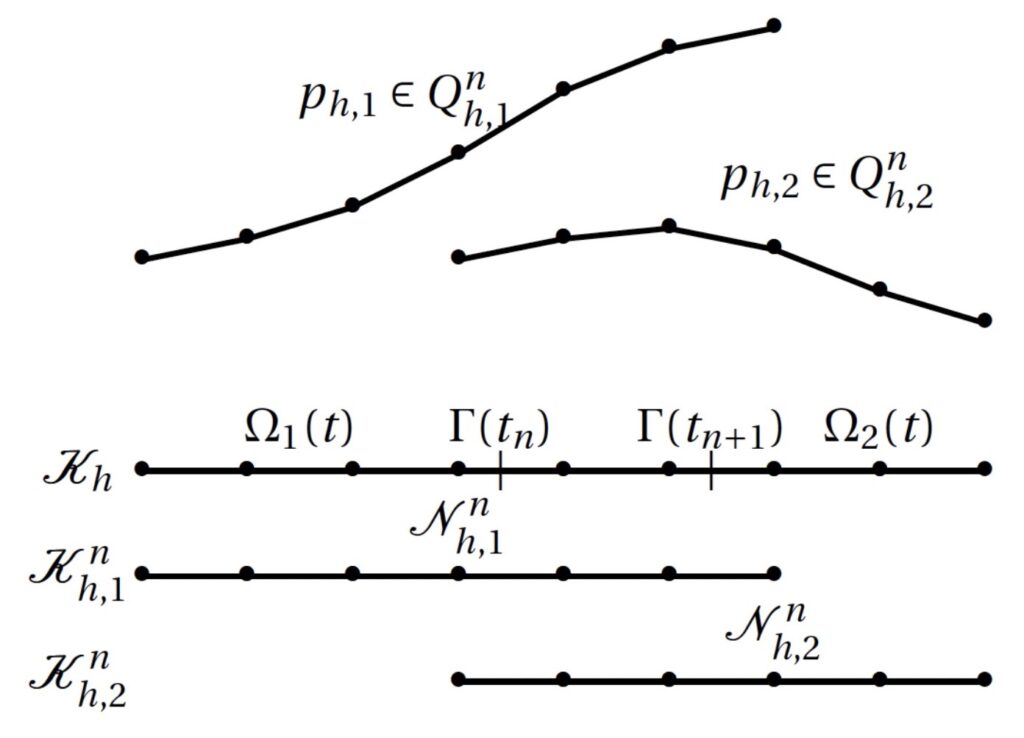
A Cut Finite Element Method (CutFEM) for the time-dependent Navier-Stokes equations involving two immiscible incompressible fluids is developed in [1]. The numerical method is able to accurately approximate a discontinuous pressure and a weak discontinuous velocity field across evolving interfaces without requiring the mesh to be fitted to the domain or regularizing the discontinuities. Discontinuous solutions across interfaces are built from two solutions one on each side of the interface with overlap on the elements cut by the interface during a time interval, see Figure. Interface conditions are imposed weakly into the variational formulation and define the discontinuous solution on the cut elements. The computational method is based on a space-time finite element formulation with discontinuous elements in time. Stabilization terms are added to the variational formulation to guarantee a stable method, well posed linear systems, and a convenient implementation based on quadrature rules in time. A new strategy for computing high order approximations to the surface tension force by computing a stabilized mean curvature vector is also proposed.
[1] Thomas Frachon, Sara Zahedi, A Cut Finite Element Method for Incompressible Two-Phase Navier-Stokes Flows, https://arxiv.org/abs/1808.02662
Fig: Illustration of the meshes and the pressure space in CutFEM associated with a time interval Inin a one space dimensional model. The interface evolves from G(tn) to G(tn+1) during the time interval In.




